Contact Sign In
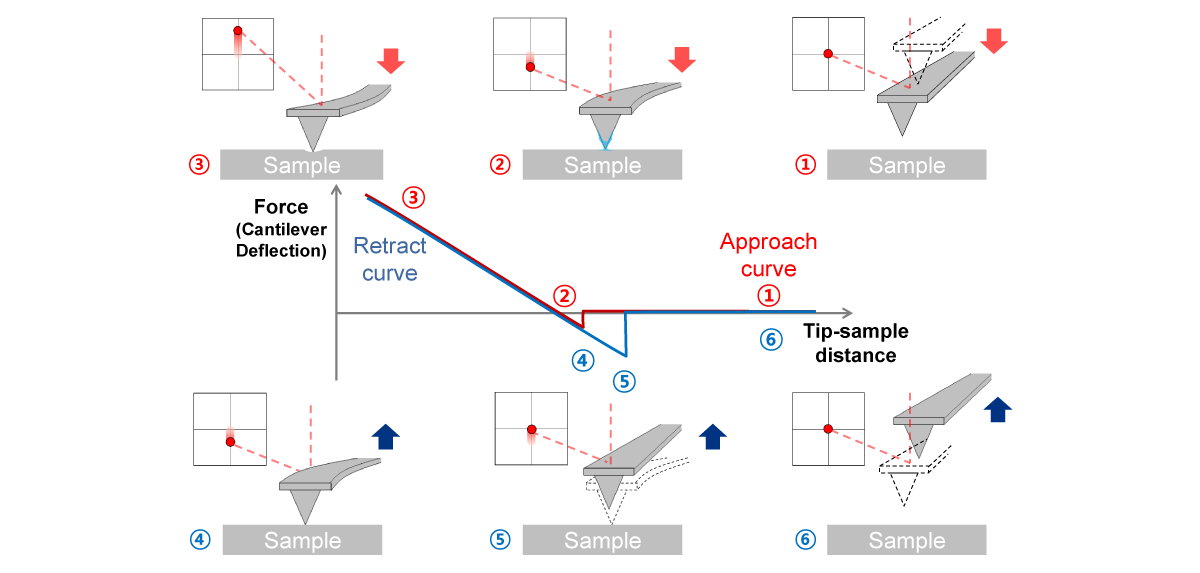
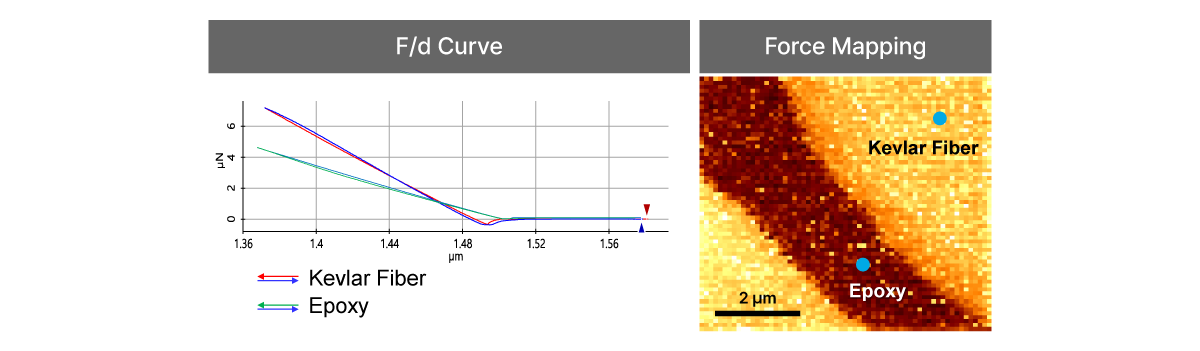
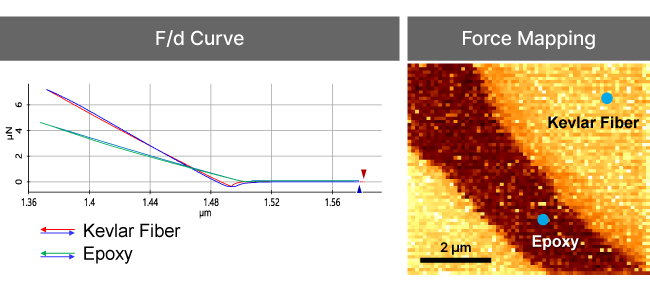
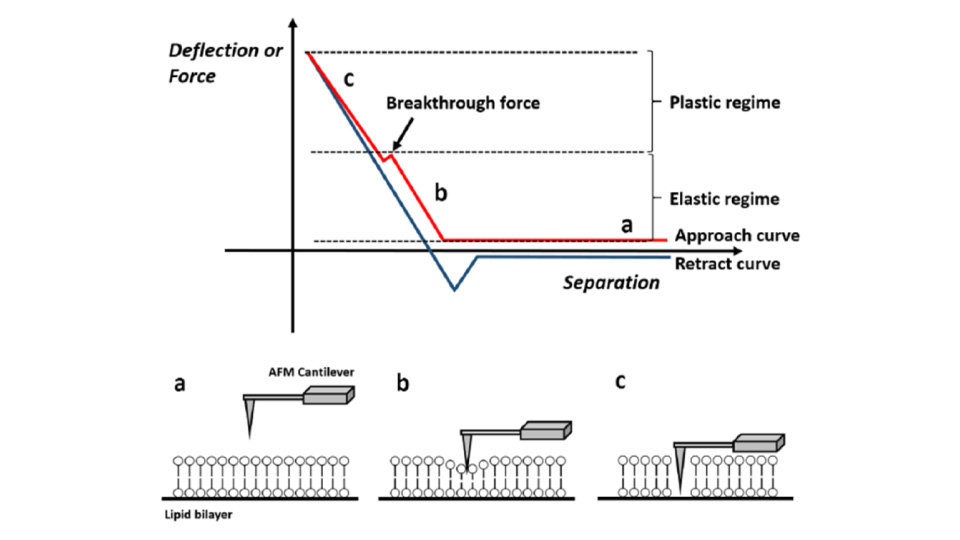
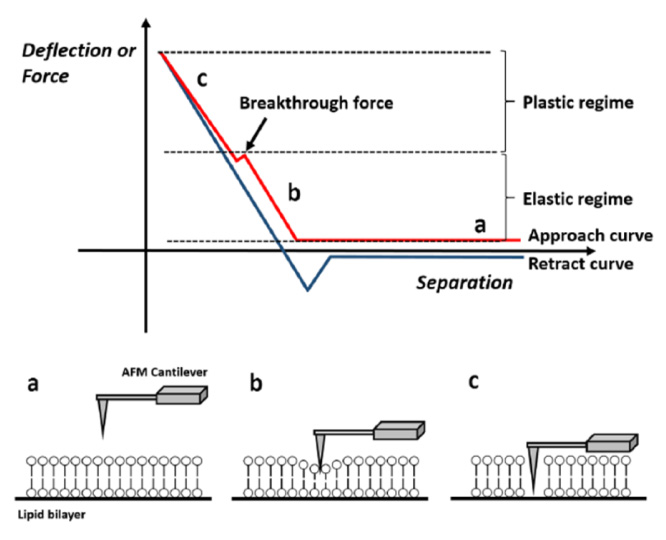
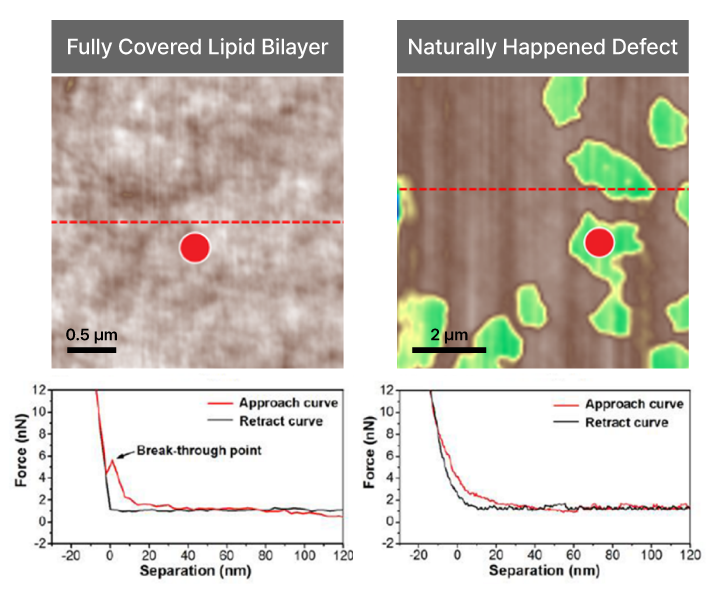
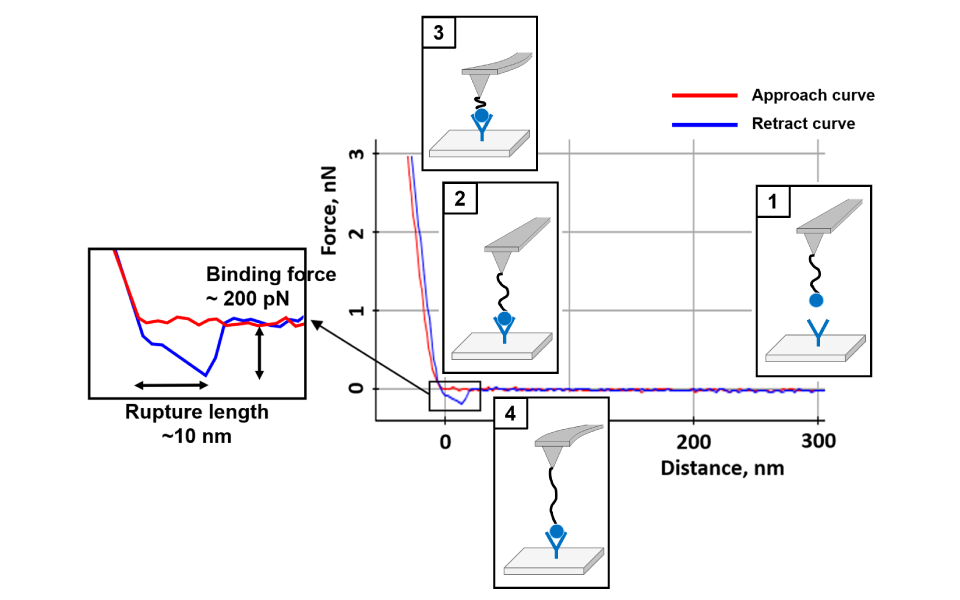
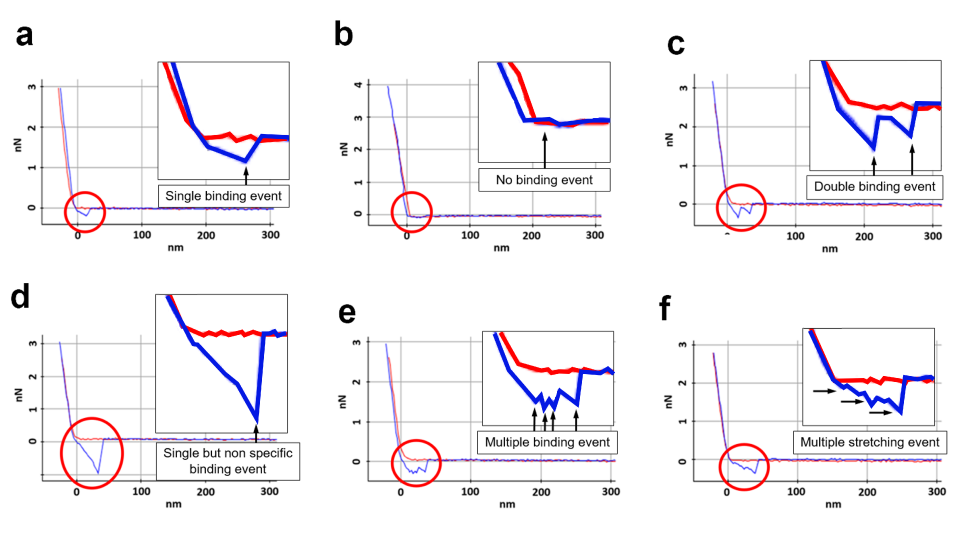
Force-distance Spectroscopy
F/d Spectroscopy
Mechanical property analysis by recording cantilever deflection relative to controlled tip–sample distance during approach and retraction cycles
Get Expert Support
What is F/d Spectroscopy
(Force-distance Spectroscopy)
F/d Spectroscopy measures detailed mechanical interactions between the AFM tip and sample by systematically controlling tip-sample separation and recording forces, providing quantitative information into modulus, adhesion, stiffness, and deformation properties at the nanoscale.
In F/d spectroscopy, the AFM tip approaches and retracts from the sample surface while recording cantilever deflection. The resulting F/d curve captures adhesive, elastic, and plastic interactions, providing information about material behavior. Force data can be converted into force-separation curves to isolate sample indentation from cantilever bending. Depending on the contact models (Hertz, DMT, JKR), the system computes mechanical parameters such as Young’s modulus by fitting the loading segment of the curve.
Reasons to Use This Mode
F/d spectroscopy is uniquely valuable because it enables measurement of localized mechanical properties at the nanoscale, capturing variations in stiffness, adhesion, and modulus within heterogeneous samples. F/d spectroscopy provides direct force curves that reveal quantitative nanomechanical characteristics, which can be spatially mapped to produce detailed mechanical property images. Its versatility spans from extremely soft biological specimens, such as cells, to much stiffer polymers. Additionally, by functionalizing the AFM tip, specific molecular interactions between the tip and sample can be probed, providing insight into chemical and biological binding forces. This makes F/d spectroscopy indispensable for correlating mechanical behavior with chemical specificity in complex materials.
Applications and Use Cases
F/d spectroscopy enables robust assessment of lipid bilayer integrity by probing mechanical responses during tip-sample interaction. Initially, no force is detected prior to contact (a). Upon engaging the bilayer, the tip traverses an elastic regime, marked by a gradual increase in force with deformation (b). As the applied load surpasses the bilayer's threshold, a distinct breakthrough event is observed, indicating a transition to the plastic regime and irreversible rupture (c). The characteristic F/d curve thus provides quantitative delineation of elastic modulus, breakthrough force, and bilayer continuity, facilitating direct confirmation of successful lipid bilayer formation and mechanical properties at defined locations.
In the fully covered lipid bilayer region, F/d spectroscopy measurements consistently reveal a characteristic breakthrough force at every measurement point, indicating intact bilayer formation. Conversely, in regions without lipid bilayer coverage, no breakthrough force is detected during F/d spectroscopy, confirming the absence of a continuous bilayer. This distinction effectively validates the presence or absence of the lipid bilayer by correlating mechanical rupture events with spatial location, demonstrating F/d spectroscopy’s capability to precisely map bilayer coverage and mechanical integrity with nanoscale resolution.
  • Sample: Lipid Bilayer
  • System: NX10
  • Scan Size: 3 µm × 3 µm, 5 µm × 5 µm
Single-molecule receptor-ligand interactions define the specificity of molecular recognition events. The receptor is immobilized on the substrate, while the ligand is covalently attached to the AFM tip (1). Upon approaching the sample, the ligand-functionalized tip contacts the receptor-containing surface, allowing complex formation (2, 3). Subsequent retraction of the tip exerts force on the bond, eventually breaking the ligand from its binding site (4). The resulting cantilever deflection is monitored, enabling calculation of the force associated with the specific molecular interaction. This process provides quantitative insight into the strength and dynamics of receptor-ligand binding at the single-molecule level.
The figure presents representative F/d curves for various molecular interactions. (a) displays a specific single-molecule binding event with characteristic rupture length; (b) shows no interaction; (c) and (e) reveal double or multiple binding from multi-domain or multivalent interactions; (d) illustrates a nonspecific binding event, typically with larger, variable forces; (f) demonstrates multiple stretching events. Only (a) reflects true single-molecule interaction—the others generally indicate undesirable binding, and their frequent occurrence may signal the need for experimental troubleshooting.